See also:
Evolution textbooks
on Introduction page
and home page. |
Strickbergers EVOLUTION (third edition) is a textbook for biology students. I like the chapters about the origin of the universe, the solar system, the earth and biological molecules (Part II 'The physical and chemical framework'). Even Fred Hoyle's panspermia theory is mentioned. It places biological evolution in its context. Something that is missing in other textbooks of evolution.
For example, there is neither oxygen nor atmosphere in Douglas Futuyma's textbook (5), while Strickberger has elaborate discussion of oxygen. What can be a more important molecule for life than oxygen? There is also a discussion of Haldane's dilemma under the heading "The Cost of Evolution and the Neutralist Argument". Several pages are devoted to the endosymbiosis theory of Lynn Margulis, and the section includes a page-long interview with Lynn Margulis (an early proponent of the endosymbiosis theory). These issues and many others make this book very relevant for the critics of evolution.
The cover of the book may look unattractive; the contents of the book is very attractive.
I have a minor ciriticism. I am puzzled by Strickberger's explanation of how evolution can produce a complex structure by a succession of selective steps (Chapter 4, The Darwinian Impact: Evolution and Religion).
 |  |
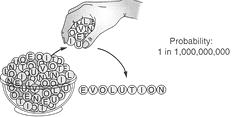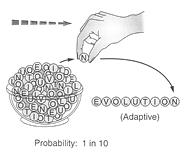| Strickberger's example-1 | example-2 final step. |
The order of amino acids in proteins frequently has been compared with the order of letters in words and sentences. Critics of evolution use the analogy to demonstrate the extreme low probability of a random origin of a specific protein (4). Strickberger uses an experiment with letters in a bowl to demonstrate that one could get the proteins observed in organisms by chance and selection with a reasonable probability. Strickberger starts his simulation experiment with a bowl containing 10 different letters A, C, E, I, L, N, O, T, U, V in equal amounts [6]. The probability of drawing all 9 letters EVOLUTION in one event is: (1/10)9 =.000000001 [example-1]. However when letters are drawn one by one and each letter increases the survival value of the whole letter sequence (despite being incomplete), then it is easy to get the word 'EVOLUTION' according to Strickberger [example-2]. He explains:
Note that once E has been drawn and survives, the chance of getting the EV combination is the 1/10 chance of drawing V and not the 1/100 chance of drawing EV together.
This is the basis of his argument. Following his argument to the last letter I assume we get:
once 'EVOLUTIO' has been drawn and survives, the chance of getting the target word 'EVOLUTION' combination is the 1/10 chance of drawing N and not the 1/1000000000 chance of drawing EVOLUTION together.
Further I suppose that example-1 corresponds to the real-life situation where intermediates don't have survival value (only the whole word), a kind of all-or-nothing situation, and example-2 corresponds to the situation that all intermediates (EV, EVO, EVOL, EVOLU, EVOLUT, EVOLUTI, EVOLUTIO) have survival value. Furthermore I suppose that every event in example-2 is separated by one or more generations.
Strickberger concludes from this example that the chances for getting the target 'EVOLUTION' in a single event is extremely small, while it can easily be produced by successive selection of adaptive combinations.
The simulation experiment itself is clear. The problems start with the extrapolation to evolution:
- total probability: Strickberger does not calculate the total probability of the string, he only states: there is a considerable chance of obtaining the word EVOLUTION. Well: that is a vague statement. What is the total probability? If we are not allowed to multiply the individual probabilities, must we add them? That would give 9/10. This method obviously leads to an absurdity: every word longer than 10 letters that could be produced would have a probability of more than 100%. The probability would become higher when the word is longer, which is also absurd. My intuition says that the probability should become lower. So I don't see how Strickberger could escape the conclusion that the total probability of the string in example-2 is also (1/10)9. As long as the frequencies of the letters in the bowl and the target sequence stay the same, the probability of arriving at the target
EVOLUTION is the same. It looks as if Strickberger proposes a system without memory: every new draw forgets about all the previous ones. Or does he want to say that the total probability is irrelevant, because each step has a reasonable chance (1/10)? Then it would be very easy indeed to create long protein chains.
- biological: apparently what he wants to say with his example-2 is that intermediates (even the shorter ones) always have survival value. Otherwise his example-2 simply would not work. But he cannot assume this, this has to be shown by evidence. Intermediates can be neutral or disadvantageous. And I think Strickberger makes a highly unrealistic assumption. It is not true for highly conserved proteins like histone-4 (1), but could be true for myoglobin, alpha-, beta-, gamma-, delta- hemoglobins (p. 260-265).
- biological: To establish the target EVOLUTION at each selection event 90% of individuals should not reproduce (or die without descendants), which is a very severe selection. This is unrealistic.
- setup: the rules of the game. The initial condition of the bowl is ten different letters (letters A and C are included to allow words like EVOCATION and ELEVATION). This could be to simplify the calculation but also gives "a reasonable probability" in each stage. When the bowl is set-up with all 26 letters the probability would decrease to 1/26. What matters of course is real life probabilities. Another simplification is the length of the target word EVOLUTION: small compared with the length of proteins (hundreds of amino acids).
- illustration: the illustration of example-1 shows a handful of letters. But a handful of 9 letters is not a sequence of 9 letters. It only contains the right letters: 1 E, 1 V, 2 O, 1L , 1 U, 1 T, 1 I, 1 N. From these 9 letters 362880 9-letter combinations ('words') can be made (2). How can an ordered sequence be produced from a handful of unordered letters? The order can only be produced by drawing letters one by one. But in that case the difference with example-2 is not clear anymore. The difference is of course that in example-1 only the complete string of 9 letters is evaluated and if the word fails, all the 9 letters are put back in the bowl and the drawing starts from scratch.
Maybe Strickberger has a valid point, but the example and illustration is confusing. The most serious objection is the problem of intermediates. The subject of the survival value of intermediates is a very old and crucial question and needs a clear treatment (3). Since it is a recurrent theme in the repertoire of the critics of evolution, he should devote more time and space to the subject. The very presence of the example indicates that he listened to some of the critics of evolution.
He also gives a collection of responses to creationist arguments (somewhat superficial and second-hand) and an interesting list of creation myths (which show that Strickberger studied the religious background of creationism), but the modern critics of evolution with non-religious technical arguments such as Michael Behe, Fred Hoyle, Michael Denton, Lee Spetner and Walter Remine are absent in his list of references. Especially, Lee Spetner (review) presented a usefull and critical discussion of the similar METHINKS IT IS LIKE A WEASEL simulation.
Notes
- See for an explanation of the histone-4 case: Mathematics of Evolution by Fred Hoyle on this site.
- that is the number of permutations of 9 objects: 9x8x7x6x5x4x3x2x1.
- see for the importance of intermediates: review of Michael Behe on this site.
- Michael Denton(1986), Hubert Yockey(1992), David Foster(1993), Dean Overman(1997), William Dembski(1999) (all reviewed on this site).
- Douglas Futuyma (1998) Evolutionary Biology, Third edition.
- 'in equal amounts': letter 'O' occurs twice in 'EVOLUTION', but not twice in his list of letters, so I suppose its frequency in the bowl is not twice as high as the rest of the letters. That complificates the example. Small modification in the text and layout have been made. Aug 19 2022
Further Reading
- Monroe Strickberger is also the author of the textbook Genetics, 1985, 3d ed.
- The homesite of Strickberger's EVOLUTION by the publisher.
- Google books.
- The fourth edition of Strickberger is edited by Brian K. Hall, and Benedikt Hallgrímsson. (including Preview Chapter 1 and Chapter 3!)
|
